10048. Reverse the graph
A directed graph
with n vertices and m edges is given, with
vertices numbered from 1 to n. Find the minimum number of
edges that need to be reversed so that there exists at least one path from
vertex 1 to vertex n.
Input. The first line
contains two integers n and m
(1 ≤ n, m ≤ 2 * 106) – the number of vertices and edges in
the graph. Each of the following m lines contains two integers xi and yi (1 ≤ xi,
yi ≤ n),
indicating that the i-th directed edge goes from vertex xi to
vertex yi
.
Output. Print the
minimum number of edges that need to be reversed. If it is not possible to
obtain a path from vertex 1 to vertex n,
print −1.
|
Sample
input |
Sample
output |
|
7 7 1 2 3 2 3 4 7 4 6 2 5 6 7 5 |
2 |
SOLUTION
breadth first search, 0-1 graph
Algorithm analysis
Ñonstruct a 0-1 graph by
assigning a weight of 0 to the existing edges and
a weight of 1 to their reversed edges. Then, run a breadth-first search.
The length of the shortest path from vertex 1 to vertex n will equal the
minimum number of edges that need to be reversed.
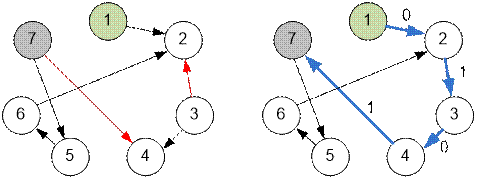
Example
The graph in the example
looks as follows:
Algorithm realization
Declare the constant infinity.
#define INF
0x3F3F3F3F
Declare the array of
shortest distances dist and the adjacency list
of the graph g. For each edge, store its
weight (0 or 1) along with the adjacent vertex.
vector<int>
dist;
vector<vector<pair<int, int>
> > g;
The bfs function implements breadth-first search
from the vertex start.
void bfs(int start)
{
dist = vector<int>(n
+ 1, INF);
dist[start] = 0;
deque<int> q;
q.push_back(start);
while (!q.empty())
{
int v = q.front(); q.pop_front();
for (auto edge : g[v])
{
int to
= edge.first;
int w =
edge.second;
if
(dist[to]
> dist[v] +
w)
{
dist[to] = dist[v] + w;
Depending on the weight of the edge w, add vertex to to
the end or the front of the queue.
if (w
== 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
The main part of the program. Read the input data.
scanf("%d %d",
&n, &m);
g.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d
%d", &a, &b);
Assign a weight of 0 to a directed edge a → b, and a weight
of 1 to the reverse edge.
g[a].push_back({ b, 0 });
g[b].push_back({ a, 1 });
}
Start the breadth-first search from the vertex 1.
bfs(1);
Print the answer – the shortest distance to vertex n.
if (dist[n] == INF)
printf("-1\n");
else
printf("%d\n",
dist[n]);